The structure of proper holomorphic maps with multiplicity higher than one from bounded Reinhardt domains in onto two-dimensional complex manifolds is described.
ISSN: 1468-4810
Izvestiya: Mathematics is the English edition of the Russian bimonthly journal Izvestiya Rossiiskoi Akademii Nauk, Seriya Matematicheskaya, founded in 1937. Izvestiya: Mathematics has been published in partnership with Turpion Ltd since 1995. The journal publishes only original research papers containing full results in the author's field of study.
A. B. Aleksandrov and V. V. Peller 2020 Izv. Math. 84 659
We consider functions  of pairs of noncommuting contractions on Hilbert space and study the problem as to which functions
of pairs of noncommuting contractions on Hilbert space and study the problem as to which functions  we have Lipschitz type estimates in Schatten–von Neumann norms. We prove that if
we have Lipschitz type estimates in Schatten–von Neumann norms. We prove that if  belongs to the Besov class
belongs to the Besov class  of analytic functions in the bidisc, then we have a Lipschitz type estimate for functions
of analytic functions in the bidisc, then we have a Lipschitz type estimate for functions  of pairs of not necessarily commuting contractions
of pairs of not necessarily commuting contractions  in the Schatten–von Neumann norms
in the Schatten–von Neumann norms  for
for ![$p\in[1,2]$](https://content.cld.iop.org/journals/1064-5632/84/4/659/revision1/IZV_84_4_659ieqn6.gif) . On the other hand, we show that for functions in
. On the other hand, we show that for functions in  , there are no such Lipschitz type estimates for
, there are no such Lipschitz type estimates for  , nor in the operator norm.
, nor in the operator norm.
A. V. Domrin 2021 Izv. Math. 85 367
In the holomorphic version of the inverse scattering method, we prove that the determinant of a Toeplitz-type Fredholm operator arising in the solution of the inverse problem is an entire function of the spatial variable for all potentials whose scattering data belong to a Gevrey class strictly less than 1. As a corollary, we establish that, up to a constant factor, every local holomorphic solution of the Korteweg–de Vries equation is the second logarithmic derivative of an entire function of the spatial variable. We discuss the possible order of growth of this entire function. Analogous results are given for all soliton equations of parabolic type.
R. I. Grigorchuk et al 2021 Izv. Math. 85 1128
The aim of this paper is to describe the structure of finitely generated subgroups of a family of branch groups containing the first Grigorchuk group and the Gupta–Sidki  -group. We then use this to show that all the groups in this family are subgroup separable (LERF).
-group. We then use this to show that all the groups in this family are subgroup separable (LERF).
These results are obtained as a corollary of a more general structural statement on subdirect products of just infinite groups.
I. A. Ivanov-Pogodaev and A. Ya. Kanel-Belov 2021 Izv. Math. 85 1146
This paper is the first in a series of three devoted to constructing a finitely presented infinite nilsemigroup satisfying the identity  . This solves a problem of Lev Shevrin and Mark Sapir.
. This solves a problem of Lev Shevrin and Mark Sapir.
In this first part we obtain a sequence of complexes formed of squares ( -cycles) having the following geometric properties.
-cycles) having the following geometric properties.
1) Complexes are uniformly elliptic. A space is said to be uniformly elliptic if there is a constant  such that in the set of shortest paths of length
such that in the set of shortest paths of length  connecting points
connecting points  and
and  there are two paths such that the distance between them is at most
there are two paths such that the distance between them is at most  . In this case, the distance between paths with the same beginning and end is defined as the maximal distance between the corresponding points.
. In this case, the distance between paths with the same beginning and end is defined as the maximal distance between the corresponding points.
2) Complexes are nested. A complex of level  is obtained from a complex of level
is obtained from a complex of level  by adding several vertices and edges according to certain rules.
by adding several vertices and edges according to certain rules.
3) Paths admit local transformations. Assume that we can transform paths by replacing a path along two sides of a minimal square by the path along the other two sides. Two shortest paths with the same ends can be transformed into each other locally if these ends are vertices of a square in the embedded complex.
The geometric properties of the sequence of complexes will be further used to define finitely presented semigroups.
M. E. Kazarian et al 2021 Izv. Math. 85 681
We study real Hurwitz numbers enumerating real meromorphic functions of a special kind, referred to as framed purely real functions. We deduce partial differential equations of cut-and-join type for the generating functions for these numbers. We also construct a topological field theory for them.
Yu. G. Prokhorov and C. A. Shramov 2020 Izv. Math. 84 978
We classify uniruled compact Kähler threefolds whose groups of bimeromorphic selfmaps do not have the Jordan property.
D. R. Gayfulin and I. D. Kan 2021 Izv. Math. 85 621
We prove new results on the derivative of the Minkowski question mark function.
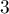 on the complex of cycles
on the complex of cyclesA. A. Gaifullin 2021 Izv. Math. 85 1060
The Torelli group of a closed oriented surface  of genus
of genus  is the subgroup
is the subgroup  of the mapping class group
of the mapping class group  consisting of all mapping classes that act trivially on the homology of
consisting of all mapping classes that act trivially on the homology of  . One of the most intriguing open problems concerning Torelli groups is the question of whether the group
. One of the most intriguing open problems concerning Torelli groups is the question of whether the group  is finitely presented. A possible approach to this problem relies on the study of the second homology group of
is finitely presented. A possible approach to this problem relies on the study of the second homology group of  using the spectral sequence
using the spectral sequence  for the action of
for the action of  on the complex of cycles. In this paper we obtain evidence for the conjecture that
on the complex of cycles. In this paper we obtain evidence for the conjecture that  is not finitely generated and hence
is not finitely generated and hence  is not finitely presented. Namely, we prove that the term
is not finitely presented. Namely, we prove that the term  of the spectral sequence is not finitely generated, that is, the group
of the spectral sequence is not finitely generated, that is, the group  remains infinitely generated after taking quotients by the images of the differentials
remains infinitely generated after taking quotients by the images of the differentials  and
and  . Proving that it remains infinitely generated after taking the quotient by the image of
. Proving that it remains infinitely generated after taking the quotient by the image of  would complete the proof that
would complete the proof that  is not finitely presented.
is not finitely presented.
V. A. Krasnov 2020 Izv. Math. 84 502
We prove some properties of real Segre cubics. In particular, we find the topological types of the real parts of Segre cubics as well as the topological types of the real parts of the complements of the Segre planes. We prove some differential-geometric properties of the real parts of real Segre cubics and Kummer quartics. We study the automorphism groups of real Segre cubics and, in particular, their action on the real parts of these cubics.
D. Jojić et al 2022 Izv. Math. 86 275
We prove a multiple coloured Tverberg theorem and a balanced coloured Tverberg theorem, applying different methods, tools and ideas. The proof of the first theorem uses a multiple chessboard complex (as configuration space) and the Eilenberg–Krasnoselskii theory of degrees of equivariant maps for non-free group actions. The proof of the second result relies on the high connectivity of the configuration space, established by using discrete Morse theory.
V. A. Krasnov 2022 Izv. Math. 86 291
The intersection of two quadrics is called a biquadric. If we mark a non-singular quadric in the pencil of quadrics through a given biquadric, then the given biquadric is called a marked biquadric. In the classical papers of Plücker and Klein, a Kummer surface was canonically associated with every three-dimensional marked biquadric (that is, with a quadratic line complex provided that the Plücker–Klein quadric is marked). In Reid’s thesis, this correspondence was generalized to odd-dimensional marked biquadrics of arbitrary dimension 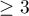 . In this case, a Kummer variety of dimension
. In this case, a Kummer variety of dimension  corresponds to every biquadric of dimension
corresponds to every biquadric of dimension  . Reid only constructed the generalized Plücker–Klein correspondence. This map was not studied later. The present paper is devoted to a partial solution of the problem of creating the corresponding theory.
. Reid only constructed the generalized Plücker–Klein correspondence. This map was not studied later. The present paper is devoted to a partial solution of the problem of creating the corresponding theory.
E. S. Baranovskii 2022 Izv. Math. 86 221
We consider the problem of the optimal start control for two-dimensional Boussinesq equations describing non-isothermal flows of a viscous fluid in a bounded domain. Using the study of the properties of admissible tuples and of the evolution operator, we prove the solubility of the optimization problem under natural assumptions about the model data. We derive a variational inequality which is satisfied by the optimal control provided that the objective functional is determined by the final observation. We also obtain sufficient conditions for the uniqueness of an optimal control.
 -structures and some of its applications
-structures and some of its applicationsV. V. Gorbatsevich 2022 Izv. Math. 86 252
We construct an analogue of classical Lie theory in the case of Lie groups and Lie algebras defined over the algebra of dual numbers. As an application, we study approximate symmetries of differential equations and construct analogues of Hjelmslev’s natural geometry.
E. K. Brusyanskaya and Ant. A. Klyachko 2022 Izv. Math. 86 243
It is well known that the number of homomorphisms from a group 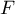 to a group
to a group  is divisible by the greatest common divisor of the order of
is divisible by the greatest common divisor of the order of  and the exponent of
and the exponent of ![$F/[F,F]$](https://content.cld.iop.org/journals/1064-5632/86/2/243/revision1/IZV_86_2_243ieqn3.gif) . We study the question of what can be said about the number of homomorphisms satisfying certain natural conditions like injectivity or surjectivity. A simple non-trivial consequence of our results is the fact that in any finite group the number of generating pairs
. We study the question of what can be said about the number of homomorphisms satisfying certain natural conditions like injectivity or surjectivity. A simple non-trivial consequence of our results is the fact that in any finite group the number of generating pairs  such that
such that 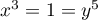 is divisible by the greatest common divisor of fifteen and the order of the group
is divisible by the greatest common divisor of fifteen and the order of the group ![$[G,G]\cdot\{g^{15}\mid g\in G\}$](https://content.cld.iop.org/journals/1064-5632/86/2/243/revision1/IZV_86_2_243ieqn6.gif) .
.
Journal links
Journal information
- 1993-present
Izvestiya: Mathematics
Online ISSN: 1468-4810
Print ISSN: 1064-5632
Journal history
- 1993-present
Izvestiya: Mathematics - 1967-1992
Mathematics of the USSR-Izvestiya



